前言

昨天我們簡介強化學習的基本概念，並在最後提到 馬可夫決策過程 。不過它有許多專有名詞與性質，今天我們先說明它的簡化版 ─ 馬可夫鏈。

馬可夫鏈 (Markov Chains)

Andrey Markov 是一名俄羅斯數學家，主要研究的興趣是隨機程序。馬可夫鏈是馬可夫在研究「一連串相關事件所組成的系統，會怎麼隨著時間變化」時，所提出的一個數學模型。這個模型中有以下部分：

• 狀態集(states)：包含所有 m 種狀態，記作
• 初始狀態(initial state)：一開始的狀態，記作
• 轉移矩陣(transition matrix)：描述上一個狀態，是如何轉移到下一個狀態的，記作

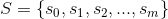
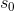
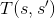
這裡的狀態是一個攏統的稱呼，可以包括許多東西，例如老鼠是 飢餓的或吃飽的、人是站著或坐著。在清楚模型組成元件後，接著來理解「一連串事件」這個部分。

馬可夫性質 (Markov Property)

馬可夫說這一連串的事件，奠基在這個性質上，並給出定義：「在狀態轉移的過程中，下一個狀態只受到現在狀態的影響，與過去狀態無關」。假設現在現在一連串事件共有 n 個，以條件機率的方式描述，可以將馬可夫性質定義為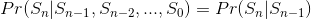

而馬可夫鏈呢，就是指這些符合馬可夫性質的事件，如同鏈子一件一件的串在一起。我們可以使用 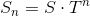計算第 n 次時，出現各狀態的機率。最終我們可以觀察到，經過許多次轉移後，各狀態出現的機率是固定的，以下舉個例子說明。

小明的狀態轉移

有個人叫小明，他平時只有兩個狀態 ─ 躺著()跟坐著()。如果我們隔一段時間觀察小明的狀態，會發現當小明原本是躺著的時候，有 90% 的機率會繼續躺著，有 10% 的機率會變成坐著；坐著的時候，有 50% 的機率會變成躺著， 50% 的機率繼續坐著。

我們可以將上述觀察到的內容，記作馬可夫鏈中的元件，方便之後運算

• 狀態：小明一開始的狀態如果是躺著，那麼我們可以記作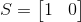

• 轉移矩陣：根據上面的描述，可以記為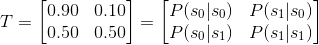

• 狀態轉移方式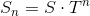： ，其中 n 表示第幾次觀察。

透過上面的狀態轉移方式，我們可以計算第 n 次觀察時，小明各狀態的機率

• 第一次觀察小明的時候，小明各狀態的機率
• 第三次觀察小明的時候，小明各狀態的機率
• 第十次之後，小明各狀態的機率就固定為

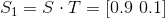
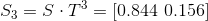
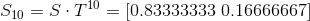
如果有興趣，可以自己用手算算看，如果覺得手算太麻煩了，那就明天用 Python 解決吧！